Grundmenge
und Definitonsmenge |
 |
Grundmenge |
|
Die Menge, aus der die Lösung einer Gleichung stammen soll, wird
Grundmenge genannt. Ist man z.B. nur an positven Lösungen einer
Gleichung interessiert, dann wählt man als Grundmenge die Menge
R+.
Wird keine Grundmenge angegeben, so ist man in der Regel an
einer Lösung aus der Menge R
interessiert.
|
 |
Definitionsmenge |
|
Die Definitionsmenge einer Menge besteht aus allen Elementen der
Grundmenge,
welche die Gleichung in eine wahre oder eine falsche Aussage übergehen
lassen.
Als Beispiel sei die Grundmenge R
und die folgende Gleichung gegeben:
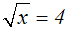
Dann besteht die Definitionsmenge aus R+
, denn für negative Zahlen ist
die Wurzel nicht definiert.
|
 |
Lösungsmenge |
|
Zur Lösungsmenge gehören alle Elemente der Definitionsmenge, welche
die
gegebene Gleichung in eine wahre Aussage überführen. Beispiel:
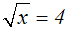
Die Lösungsmenge lautet: L={16}.
|
|
|
|