Multiplikation mit
einem Term, der die Unbekannte x enthält. |
 |
Satz |
|
Die
Multiplikation mit einem Term, in dem die unbekannte Variable x
auftaucht,
ist keine Äquivalenzumformung, denn es könnte eine versteckte
Multiplikation
mit der Zahl Null stattfinden. |
|
|
|
 |
Beispiel |
|
Das folgende Beispiel zeigt, dass bei einer
Multiplikation mit einem Term,
der die unbekannte Variable x enthält, Lösungen hinzukommen können:

|
 |
Satz |
|
Die
Multiplikation mit einem Term, in dem die unbekannte Variable x
auftaucht,
ist nur dann eine Äquivalenzumformung,
wenn der Term nicht den Wert Null
annehmen kann (weil der Definitionsbereich dies nicht zuläßt). |
|
|
|
|
 |
Erlärung |
|
Auch hier wird wieder mit x multipliziert. Weil
jedoch x nicht Null werden kann
(x liegt nicht im Definitionsbereich), handelt es sich um eine
Äquivalenzumformung.
Es entstehen zwar falsche Ergebnisse (hier: x=0) bei der Multiplikation
mit dem Term,
doch da diese nicht im Definitionsbereich liegen, sind sie nicht Teil
der Lösungsmenge:
 |
|
|
|
 |
Satz |
|
Die
Multiplikationen mit Termen, welche die unbekannte Variable x
enthalten,
ist eine Äquivalenzumformung, wenn der Term nicht zu Null werden
kann,
weil er der Nenner eines Bruches ist, und zuvor der Definitionsbereich
der Gleichung bestimmt wurde.
|
|
|
|
|
 |
Erklärung |
|
Die Multiplikation mit einem Term, der die
unbekannte Variable x enthält, ist in der
Praxis nur dann nötig, wenn man eine Bruchgleichung lösen
will, wie z.B. die folgende:
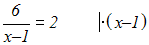
Nun könnte man auf die Idee kommen, einfach die Zahl "1" aus dem
Definitionsbereich
zu entfernen. Dadurch würde könnte der Term (x–1) nicht zu Null werden
können,
und wir dürfen mit ihm multiplizieren, ohne das Lösungen hinzukommen
oder verlorengehen.
Dies ist jedoch weder erlaubt noch nötig:
Es ist nicht erlaubt, weil man den Definitionsbereich
nicht einfach einschränken kann,
nur um die "Multiplikation mit einem Term" zu einer
Äquivalenzumformung zu machen.
Schränkt man den Definitionsbereich einer Gleichung nämlich willkürlich ein,
dann handelt
es sich (streng genommen) um eine andere Gleichung, denn eine
Gleichung besteht aus
zwei Termen, einem Gleichheitszeichen und der Angabe des
Definitionsbereiches!
Es ist aber auch nicht nötig, den Definitionsbereich
einzuschränken, denn wir
multiplizieren hier mit einem Nenner eines
Bruchterms. Der Nenner eines Bruchtermes
kann jedoch nicht zu Null werden. Der erste Schritt beim Lösen einer Bruchgleichung
besteht nämlich darin, alle
Zahlen aus dem Definitionsbereich der Gleichung zu streichen,
bei denen der Nenner eines Bruchterms zu Null wird (Grund: Division durch Null ist nicht
erlaubt).
|
 |
Zusammenfassung
der Seite |
| |
Die Multiplikation mit Termen, in denen die unbekannte Variable x
auftritt, ist keine Äquivalenzumformung, weil eine versteckte
Multiplikation mit Null auftreten kann.
Dies spielt in der Praxis beim Lösen von Gleichungen jedoch keine
Rolle,
weil man in der
Praxis nur mit den Nennern von Bruchtermen
multipliziert,
und die Nenner von Bruchtermen
nicht Null werden können, wenn man - wir es
Vorschrift ist -
vor dem Lösen der Gleichung
den Definitionsbereich der Gleichung
bestimmt. |
|
| |
|
|