Prinzipiell bleibt die Lösungsmenge einer Gleichung unverändert, wenn man Term-
umformungen anwendet, denn Termumformungen verändern die Lösungsmenge nicht.
Während man jedoch bei den Regeln der Klammerrechnung nicht aufpassen muß, wird bei
Termumformungen durch Rechengesetze meist nicht auf den Definitionsbereich der Gesetze
geachtet, und es kommt zum Verlust von Lösungen oder zu Scheinlösungen. Beispiel:
  
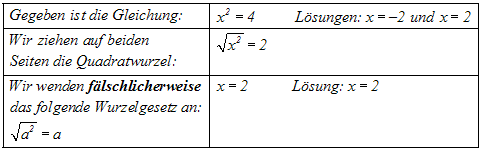
Hier geht eine Lösung (x=–2) verloren, weil wir ein Wurzelgesetz angewendet
haben, dass nur für nicht-negative a gilt.

Es können aber auch Lösungen hinzukommen, wie das folgende Beispiel zeigt:


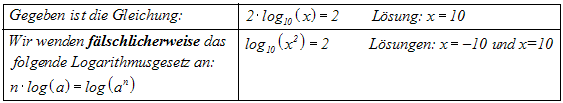
Hier kommt eine Lösung (x=–10) hinzu, weil wir ein Logarithmusgesetz
angewendet haben, dass nur für nicht-negative a gilt.
Dadurch wurde der Definitionsbereich vergrößert, und eine Vergrößerung
des Definitionsbereiches kann zu Scheinlösungen führen.