Wir haben bereits gezeigt, dass z.B. die Grundrechenarten (Addition, Subtraktion,
Multiplikation mit einer Zahl ungleich Null, Division mit einer Zahl ungleich Null)
eine Äquivalenzumformung darstellen. Beispielsweise ist die Addition der Zahl 3
auf beiden Seiten der Gleichung eine Äquivalenzumformung:
  

  
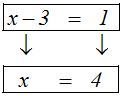
Es gibt aber auch Äquivalenzumformungen, bei denen man nur eine Seite der Gleichung
ändert. Es sind die sogenannten Termumformungen. Dabei wird eine Seite der
Gleichung durch das Anwenden eines Rechengesetzes verändert. Beispiel:
  

  
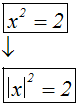
Weil durch die Anwendung des Rechengesetzes ein gleichwertiger Term entsteht
(die Terme haben auf der linken Seite haben den gleichen Wert, unabhängig davon,
welche Zahl man einsetzt), verändert sich auch die Lösungsmenge der Gleichung nicht.
Termumformungen sind daher auch Äquivalenzumformungen.