Im vorigen Kapitel hatten wir Gleichungen gelöst, indem wir die elementaren
Äquivalenzumformungen 1.Addition, 2.Subtraktion, 3.Multiplikation und 4.Division anwendeten. Beispiel:
 
       
 
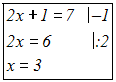
Durch diese vier Äquivalenzumformungen lassen sich aber nicht alle Gleichungen lösen.
Ist die Variable x nämlich Argument einer Funktion, so kann sie nicht durch diese vier
elementaren Äquivalenzumformungen isoliert werden. Beispiel:
  
    
  
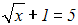
Man könnte in diesem Beispiel auf beiden Seiten der Gleichung "1" subtrahieren:
  
  
  
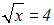
Nun kommen wir aber nicht weiter, denn wir können das Wurzelzeichen nicht beseitigen,
weder durch Addition, Subtraktion, Multiplikation oder Division. Und weil wir das
Wurzelzeichen nicht beseitigen können, können wir x nicht isolieren um dadurch
die Gleichung zu lösen.

Wir brauchen dazu einen neuen Typ von Äquivalenzumformungen: 
Das Anwenden einer injektiven Funktion. Mit diesem Typ von
Äquivalenzumformungen beschäftigt sich dieses Kapitel.