Eine nicht-injektive
Funktion anwenden ist
eine Folgeumformung (Implikation) |
 |
Satz |
| |
Macht man beide
Seiten einer Gleichung zum Argument einer nicht-injektiven Funktion,
dann ist dies keine Äquivalenzumformung, sondern eine Folgeumformung
(Implikation),
d.h. es können Scheinlösungen entstehen.
Die Scheinlösungen kann man aber durch eine
Probe herausfiltern.
Natürlich muss die nicht-injektive Funktion wieder einen ausreichend großen
Definitionsbereich haben,
damit nicht ein undefinierter Ausdruck entsteht. |
|
| |
|
 |
Erklärung |
|
Wir betrachten die folgende Funktion; sie hat die
Lösungsmenge {5}:
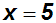
Nun quadrieren wir die Gleichung, d.h. wir machen beide Seiten der
Gleichung
zum Argument
der Quadratfunktion, die eine nicht-injektive Funktion ist:
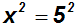
Wir vereinfachen:
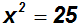
Zur Lösungsmenge L={5}
ist eine sogenannte
"Scheinlösung" hinzugekommen,
nämlich die Zahl –5. Man kann
Scheinlösungen aber
erkennen, indem man sie
in die ursprüngliche Gleichung einsetzt. d.h. indem man die Probe macht:
Setzt
man –5 in die
erste Gleichung ein, so erhält man die unwahre Aussage –5=5,
und somit
ist –5 keine
Lösung der ursprünglichen Gleichung, sondern eine Scheinlösung. |
|