Gleichungen
Potenzfunktionen
mit geradem Exponent
a-absatz.pcx (280 Byte) Fall 1: Eine Seite ist positiv
Gegeben ist eine Gleichung, in der eine Potenzfunktion mit geradem Exponent
vorkommt, im Beispiel die Quadratfunktion:

  

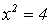
Am besten wäre es nun, die Umkehrfunktion der Quadratfunktion anzuwenden,
doch die Quadratfunktion hat nur eine Umkehrrelation: Die Quadratwurzelrelation.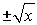
Man könnte sie zwar prinzipiell anwenden, doch wir wenden stattdessen die
Quadratwurzelfunktion an.
 
  

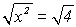
Zuerst überlegen wir uns, ob dies eine Äquivalenz- oder Folgeumformung ist,
oder eine unerlaubte Umformung:

    Der Definitionsbereich der Wurzelfunktion ist R+, und die beiden Seiten der Gleichung
    sind positiv (auch die linke Seite, denn eine Potenz mit geradem Exponent ist stets positiv).
    Somit ist die Umformung erlaubt. Weil die Wurzelfunktion außerdem injektiv ist, handelt
    es sich um eine Äquivalenzumformung.

Nun wollen wir die linke Seite der Gleichung vereinfachen. Dazu wenden wir ein
Gesetz über Beträge an. Der Satz lautet: 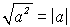. Durch diese Termumformung
erhalten wir die Betragsgleichung:

    

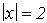
Diese Betragsgleichung hat die Lösungen x=2 und x=–2.Weil wir nur
Äquivalenzumformungen vorgenommen haben, sind dies auch die
Lösungen der ursprünglichen Gleichung, die gegeben war.
a-absatz.pcx (280 Byte) Fall 2: Eine Seite ist negativ
Im Fall 2 steht auf einer Seite der Gleichung eine negative Zahl.
In diesem Fall hat die Gleichung keine Lösung, denn auf der einen Seite
steht eine gerade Potenz, und diese ist stets positiv, aber auf der anderen
Seite steht eine negative Zahl:
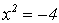
a-absatz.pcx (280 Byte) Alternative Lösungsmethode (nur für Lehrer)
Diese Methode wird in den Übungsaufgaben nicht verwendet.
Die Methode ist nur für Theoretiker, und zum weiteren Verständnis unnötig.

Wir teilen den Definitionsbereich der gegebenen Potenzfunktion in zwei Teile
(positiven und negativen Teil). Wir definieren die Funktion also stückweise:



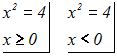
Wir haben jetzt zwei injektive Funktionen, und die haben stets eine Umkehrfunktion:
Die Umkehrfunktionen lauten:



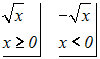
Wir wenden die Umkehrfunktionen an:



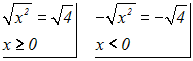
Die linken Seite der Gleichungen vereinfachen sich zu x, weil wir ja jeweils
die Umkehrfunktion angewendet haben:

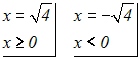Wir erhalten die beiden Lösungen x=2 und x–2. Es gilt also:  L={–2,2}