Potenzfunktionen
mit ungeradem Exponent |
 |
Fall 1: Die Konstante ist positiv |
|
Gegegen ist eine Gleichung, in der eine Potenzfunktion mit ungeradem
Exponent
vorkommt,
im Beispiel die Kubikfunktion:
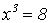
Wir wenden die Kubikwurzelfunktion an:
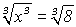
Zuerst überlegen wir uns, ob dies eine Äquivalenz- oder Folgeumformung
ist,
oder eine unerlaubte Umformung:
Der Definitionsbereich der Kubikwurzelfunktion ist R+
Wir müssen daher überprüfen, ob beide Seiten
der Gleichung nicht-negativ sind.
Die rechte Seite der gegebenen
Seite (die Zahl 8) ist auf jeden Fall positiv.
Damit ist auch die linke Seite positv, denn zwischen beiden
Seiten steht das
Gleichheitszeichen. Die Umformung ist also eine erlaubte
Umformung.
Zweitens ist die Wurzelfunktion injektiv ist, und somit
handelt es sich um
eine Äquivalenzumformung.
Nun wollen wir die linke Seite der Gleichung vereinfachen. Wir überlegen
uns zuerst,
dass x nicht-negativ sein muss, denn wäre x negativ, dann wäre die linke
Seite der
gegebenen Seite negativ, die rechte Seite aber positiv.
Weil x nicht-negativ ist, dürfen wir das Wurzelgesetz:
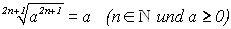
anwenden. Durch diese Termumformung erhalten wir die Gleichung:
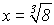
Wir rechnen die rechte Seite aus, und erhalten die Lösung x=2.
Weil wir nur
Äquivalenzumformungen vorgenommen haben, ist dies auch die
Lösung der ursprünglichen Gleichung, die gegeben war.
|
 |
Fall 2: Die Konstante ist negativ |
|
Gegegen ist eine Gleichung, in der eine Potenzfunktion mit ungeradem
Exponent
vorkommt,
im Beispiel die Kubikfunktion. Diesmal ist die rechte Seite aber
negativ:
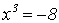
Die Kubikwurzelfunktion können wir nicht anwenden, denn man kann aus
einer negativen
Zahl kein Wurzel ziehen. Damit wir die Kubikwurzelfunktion anwenden
können, müssen
wir daher vorher die Gleichung quadrieren.
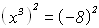
Zuerst überlegen wir uns, ob dies eine Äquivalenz- oder Folgeumformung
ist,
oder eine unerlaubte Umformung:
Die Umformung ist erlaubt, denn die Quadratfunktion hat den
Definitionsbereich R.
Zweitens ist die Quadratunktion nicht-injektiv
ist, und somit handelt es sich um
eine Folgeumformung.
Die rechte Seite rechnen wir aus, die linke Seite können wir mit einem
Potenzgesetz
vereinfachen. Das Potenzgesetz lautet
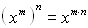 . .
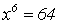
Nun liegt eine Potenzgleichung mit geradem Exponenten vor, und wir
können wie im
Beispiel auf der vorigen Seite. Wir ziehen zuerst auf beiden Seiten die
6.Wurzel:
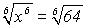
Nun wollen wir die linke Seite der Gleichung vereinfachen. Dazu wenden
wir ein
Gesetz über Beträge an.
Der Satz lautet: 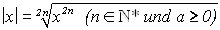 . .
Durch diese Termumformung
erhalten wir die Betragsgleichung:
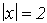
Diese Betragsgleichung hat die Lösungen x=2 und x=–2.Weil wir am
Anfang der
Rechnung den Trick mit dem Quadrieren angewendet haben, und Quadrieren
eine Folgeumformung ist, müssen wir die Probe machen. Wir setzen dazu
die
Ergebnisse in die ursprüngliche Gleichung ein. Die Probe ergibt, dass
nur x=–2
eine Lösung der Gleichung ist.
|
|