Gegegen ist eine Gleichung, in der eine Wurzelfunktion mit ungeradem Exponent vorkommt,
im Beispiel die Kubikwurzelfunktion:
  
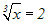    mit dem Definitionsbereich: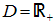
  
Wir wenden die Kubikfunktion an, d.h. wir potenzieren beide Seiten mit 3:
  
    
  
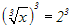
Zuerst überlegen wir uns, ob dies eine erlaubte Umformung, oder eine nicht erlaubte,
weil sie auf einen undefinierten Ausdruck führt. Ist die Umformung erlaubt, dann müssen
wir noch überlegen, ob es eine Äquivalenz- oder Folgeumformung (Implikation) ist:
  
    Der Definitionsbereich der Kubikfunktion ist R, also größer als der Wertebereich
    der Wurzelfunktion. Somit kann kein undefinierter Ausdruck entstehen, und daher
    ist die Umformung eine erlaubte Umformung. Außerdem ist die Kubikfunktion bijektiv,
    und somit handelt es sich um eine Äquivalenzumformung.
  
Nun wollen wir die linke Seite der Gleichung vereinfachen. Wir überlegen uns zuerst,
dass x nicht-negativ sein muss, denn wäre x negativ, dann wäre die Wurzel nicht definiert.
Weil x nicht-negativ ist, dürfen wir das folgende Wurzelgesetz anwenden:
  
   
  
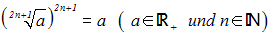
Durch diese Termumformung erhalten wir die Gleichung:
  
  
  
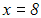
Eine Probe ist nicht nötig, da wir nur Äquivalenzumformungen durchgeführt haben.
Wir müssen jedoch prüfen, ob die Lösung im Definitionsbereich liegt, denn wir haben das
Wurzelgesetz ja nur anwenden dürfen, unter der Voraussetzung, dass x größer oder gleich
Null ist, was dadurch als sicher angenommen wurde, dass x tatsächlich im Definitionsbereich
der ursprünglichen Funktion liegt.