|
Exponentialfunktion |
 |
Beispiel |
|
Gegeben sei eine Gleichung, in der x im Exponenten einer Potenz
auftritt:
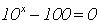
Zuerst isolieren wir den Term, in dem x im Exponenten auftritt:
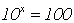
Jetzt wenden wir auf beiden Seiten die Umkehrfunktion an, also die Logarithmusfunktion
(dies ist erlaubt, denn die Logarithmusfunktion ist injektiv).
Konkret bedeutet dies, dass wir beide
Seiten
der Gleichung zum Argument der
Logarithmusfunktion machen. Als Logarithmusbasis wählen wir die Basis
der Potenz (10):
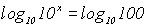
Auf der linken Seite hebt die Logarithmusfunktion die
Exponentialfunktion auf,
so wie wir es im Kurs "Umkehrfunktionen" und im Kapitel 2 gelernt haben:
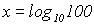
Wenn wir jetzt noch die rechte Seite der Gleichung ausrechnen,
erhalten wir
die Lösung x=2:
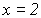
Da wir nur Äquivalenzumformungen
durchgeführt haben, ist x=2 auch die Lösung der
ursprünglichen Gleichung. Es fehlen also keine Lösungen und es sind auch keine
Scheinlösungen
hinzugekommen.
|
|