|
Motivation |
 |
Motivation |
|
Auf der vorigen Seite haben wir gezeigt, wie man eine Gleichung
vereinfachen kann,
indem man eine auftretende Funktion durch ihre Umkehrfunktion beseitigt.
Das Problem ist nun, dass man zu den elementaren Funktionen nur schwer
eine Umkehrfunktion angeben kann. Die elementaren Funktionen lauten:
Potenzfunktion mit geradem Exponenten
‚
Potenzfunktion mit ungeradem Exponenten
ƒ
Wurzelfunktion
Funktion hat überhaupt keine
Umkehrfunktion sondern nur eine Umkehrrelation,
nämlich die Wurzelrelation. Obwohl man auch diese benutzen
könnte, ist es üblich einen
Trick zu benutzen, sodass man statt der Wurzelrelation die
Wurzelfunktion anwenden kann.
Funktion ‚ hat die unheimlich
komplizierte Umkehrfunktion
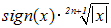
Wir werden einen Trick zeigen, wie man ohne sie auskommen kann.
Funktion ƒ hat als Umkehrfunktion
die "eingeschränkte Potenzfunktion", d.h. eine
Potenzfunktion, deren Definitionsbereich auf die nicht-negativen Zahlen
eingeschränkt ist.
Dummerweise existiert für diese Funktion kein Symbol, und daher
müssen wir
zeigen, wie man stattdessen die "normale" Potenzfunktion benutzen kann.
|
| |
|
| |
|
|