Ist Radizieren eine
Äquivalenzumformung? |
 |
Erklärung |
|
Oft liest man in Büchern, dass Radizieren keine Äquivalenzumformung sei
weil Lösungen verloren gehen können. Als Beispiel wird folgende Rechnung
angegeben:

Die Lösung geht jedoch nicht, wie in den Büchern behauptet, beim
Radizieren verloren, denn sowohl die erste als auch die zweite Gleichung
haben die gleiche Lösungsmenge: L={–2,2}.
Die Lösung geht erst zwischen der zweiten und dritten Gleichung
verloren.
Der Grund: Potenzieren und Radizieren heben sich nicht auf, denn die
Wurzelfunktion
ist nicht die Umkehrfunktion der Potenzfunktion, sondern nur die
Umkehrfunktion
der eingeschränkten Potenzfunktion (d.h. der Definitonsbereich
ist auf R+ eingeschränkt).
Die richtige Rechnung haben wir bereits kennengelernt: Man wendet ein
Gesetz über Beträge an:
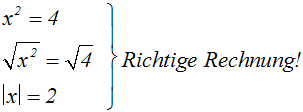
Die Aussage, dass Radizieren keine Äquvalenzumformung sei, ist also
falsch.
Radizieren ist, wie das Anwenden aller injektiven Funktionen, eine
Äquivalenzumformung,
(wobei selbstverständlich kein undefnierter Ausdrück entstehen
darf).
|
|