Überblick über alle
Lösungsmethoden geordnet nach
Funktionstyp der
auftritt |
 |
Potenzgleichung mit geradem Exponent |
|
Gegeben ist eine Potenzgleichung, deren Potenz einen geraden Exponent
hat.
Wir unterscheiden zwei Fälle:
Fall 1: Die Seite mit der Konstanten ist positiv
Gegeben sei beispielsweise folgende Gleichung:
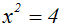
Wir radizieren beide Seiten der Gleichung mit dem Exponenten der Potenz,
also in unserem Fall mit zwei (Radizieren ist Äquivalenzumformung):
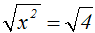
Wir wenden das folgende Gesetz an (es gibt zwei Schreibweisen):
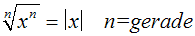 oder oder
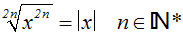
Wir erhalten die Betragsgleichung:
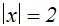
Die Lösungen der Betragsgleichung sind auch die Lösungen der gegebenen
Gleichung,
denn wir haben nur Äquivalenzumformungen durchgeführt:
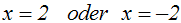
Fall 2: Die Seite mit der Konstanten ist negativ
Die Gleichung kann keine Lösung haben, da eine gerade Potenz stets
nicht-negative
Werte hat:
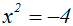
|
 |
Potenzgleichung mit ungeradem Exponent |
|
Gegeben ist eine Potenzgleichung, deren Potenz einen ungeraden Exponent
hat.
Wir unterscheiden zwei Fälle:
Fall 1: Die Seite mit der Konstanten ist positiv
Gegeben sei beispielsweise folgende Gleichung:
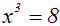
Wir radizieren beide Seiten der Gleichung mit dem Exponenten der Potenz,
also in unserem Fall mit drei (Radizieren ist eine Äquivalenzumformung):
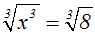
Wir wenden das folgende Gesetz an (es gibt zwei Schreibweisen):
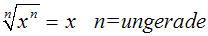 oder oder
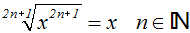
Die Lösung ist auch die Lösung der gegebenen Gleichung, denn wir haben
nur Äquivalenzumformungen durchgeführt:
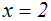
Fall 2: Die Seite mit der Konstanten ist negativ
Gegeben sei beispielsweise folgende Gleichung:
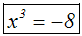
Hier würde Radizieren auf einen undefinierten Ausdruck führen,
daher dürfen wir nicht radizieren:
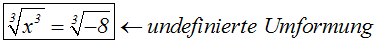
Stattdessen quadrieren wir beide Seiten der Gleichung
(Folgeumformung!):
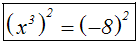
Wir vereinfachen die linke Seite mit Hilfe des Potenzgesetzes:
"Man potenziert eine Potenz, indem man die Exponenten multipliziert":
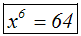
Nun haben wir eine Potenzgleichung mit geraden Exponenten, die
wir wie oben
erklärt lösen: Wir radizieren mit dem Wurzelexponent:
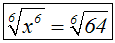
Wir wenden das folgende Gesetz an (es gibt zwei Schreibweisen):
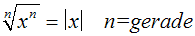 oder oder
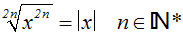
Wir erhalten:
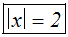
Die beiden Lösungen der Betragsgleichung lauten:
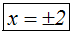
Weil wir auch eine Folgeumformung vorgenommen haben, müssen
wir die Probe machen, d.h. sowohl x=2 als auch x=–2 in die ursprüngliche
Gleichung einsetzen. Die Probe ergibt, dass nur x=–2 eine Lösung ist:
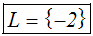 |
 |
Wurzelgleichung mit geradem Exponent |
|
Gegeben ist eine Potenzgleichung, deren Potenz einen geraden Exponenten
hat.
Wir unterscheiden zwei Fälle:
Fall 1: Die Seite mit der Konstanten ist positiv
Gegeben sei beispielsweise folgende Gleichung:
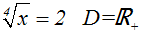
Wir potenzieren die Gleichung mit dem Wurzelexponenten.
Weil der Wurzelexponent gerade ist, ist dies eine Folgeumformung:
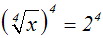
Weil laut Definitionsbereich die Unbekannte x eine nicht-negative Zahl
sein muss,
dürfen wir das folgende Gesetz anwenden:
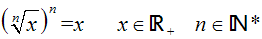
Wir erhalten die Lösung:
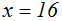
Weil wir mit einem geraden Exponenten potenziert haben, müssen wir die
Probe machen.
Die Probe ergibt, dass x=16 tatsächlich eine Lösung der Gleichung ist.
Fall 2: Die Seite mit der Konstanten ist negativ
Gegeben sei beispielsweise folgende Gleichung:
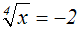
Die Gleichung kann keine Lösung haben, weil eine Wurzel nie negativ ist.
|
 |
Wurzelgleichung mit ungeradem Exponent |
|
Gegeben ist eine Potenzgleichung, deren Potenz einen ungeraden
Exponenten hat.
Wir unterscheiden zwei Fälle:
Fall 1: Die Seite mit der Konstanten ist positiv
Gegeben sei beispielsweise folgende Gleichung:
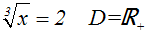
Wir potenzieren die Gleichung mit dem Wurzelexponenten.
Weil der Wurzelexponent ungerade ist, ist dies eine Äquivalenzumformung:
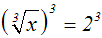
Weil laut Definitionsbereich die Unbekannte x eine nicht-negative Zahl
sein muss,
dürfen wir das folgende Wurzelgesetz anwenden:
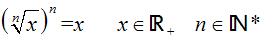
Wir erhalten die Lösung:
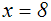
Weil wir bei der Anwendung des Wurzelgesetzes vorausgesetz haben,
dass x eine Zahl aus dem Definitionsbereich ist, müssen wir überprüfen,
ob x tatsächlich im Definitionsbereich liegt. Weil x=8 tatsächlich im
Definitionsbereich liegt, ist x=8 tatsächlich eine Lösung.
Anmerkung: Eine Probe ist nicht nötig!
Fall 2: Die Seite mit der Konstanten ist negativ
Gegeben sei beispielsweise folgende Gleichung:
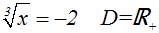
Die Gleichung kann keine Lösung haben, weil eine Wurzel nie negativ ist.
|
 |
Exponentialgleichung |
|
Gegeben ist eine Exponentialgleichung. Wir unterscheiden zwei Fälle:
Fall 1: Die Seite mit der Konstanten ist positiv
Gegeben sei beispielsweise folgende Gleichung:
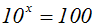
Wir logarithmieren beide Seiten mit der Basis der Potenz: Dies ist eine
definierte
Umformung, weil weil eine Potenz mit positiver Basis niemals negativ
werden kann.
Weil die Logarithmusfunktion bijektiv ist (streng monoton steigend
bzw. fallend),
handelt es sich auch um eine Äquivalenzumformung:
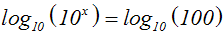
Auf der linken Seite heben sich die beiden Funktionen gegenseitig auf,
denn die
Logarithmusfunktion ist die Umkehrfunktion der Exponentialfunktion. Die
rechte
Seite der Gleichung kann man ausrechnen:
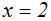
Da wir nur Äquivalenzumformungen und keine Folgeumformungen vorgenommen
haben,
brauchen wir keine Probe machen.
Fall 2: Die Seite mit der Konstanten ist negativ
Gegeben sei beispielsweise folgende Gleichung:
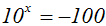
Die Gleichung kann keine Lösung haben, weil eine Potenz mit positiver
Basis
niemals negativ werden kann.
|
 |
Logarithmusgleichung |
|
Gegeben ist eine Logarithmusgleichung:
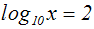
Wir erheben beide Seiten der Gleichung in den Exponenten:
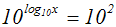
Auf der linken Seite der Gleichung heben sich Logarithmieren und
Exponentieren
(in den Exponenten erheben) gegenseitig auf. Die rechte Seite der
Gleichung
kann man ausrechnen:
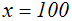
Da wir nur Äquivalenzumformungen und keine Folgeumformungen vorgenommen
haben,
brauchen wir keine Probe machen.
|
|