Unbestimmte
Ausdrücke
der Form 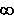 - -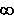 |
 |
Der unbestimmte Ausdruck  |
|
Wir betrachten nun den unbestimmten Ausdruck 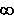 - -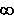
Als Beispiel wählen wir den Grenzwert:

Beide Teilfunktionen gehen gegen unendlich, wenn x gegen 0 geht:

Wir versuchen wieder, den Grenzwert graphisch zu ermitteln,
indem wir die Teilfunktionen in der Nähe von x=0 betrachten.
Dazu vergrößern wir das Bild sehr stark. Die Graphen der
Teilfunktionen erscheinen nun wie Geraden:

Man erkennt in der Vergrößerung des Bildes, daß die Teilfunktionen
den Abstand 0.5 behalten, wenn man sich dem Punkt x=0 nähert.
Daher ist der Grenzwert der Funktion (für x 0) gleich 0.5 : 0) gleich 0.5 :

|
|