Häufiger Fehler
bei
unbestimmten
Ausdrücken
der Form 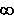 / /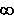 |
 |
Häufiger Fehler |
|
Nun könnte man fälschlicherweise glauben, der
Grenzwert eines
unbestimmten Ausdrucks 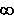 / /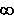 sei stets 1, denn die Division sei stets 1, denn die Division
gleicher Zahlen ergibt ja stets 1. Beispiele: 5:5=1 , 7:7=1 usw.
Betrachten wir zur Widerlegung dieser Behauptung den Grenzwert:

Zähler und Nenner gehen zwar beide gegen 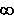 , aber Zähler und , aber Zähler und
Nenner sind nirgendwo gleich. Der Zähler ist nämlich stets
doppelt so groß wie der Nenner (siehe Bild und Formel),
und deshalb ist der Grenzwert im Unendlichen ebenfalls 2:

|
 |
Sonderfall |
|
Natürlich kann es auch sein, daß der Grenzwert
eines
unbestimmten Ausdrucks der Form 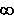 / /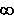 durch Zufall den durch Zufall den
Wert 1 hat. Betrachten wir als Beispiel den Grenzwert:

Die Graphen von Zähler (fz) und Nenner (fn) schmiegen sich im
Unendlichen aneinander an, d.h. sie haben im Unendlichen gleiche
Funktionswerte, und daher hat der Quotient dort den Wert 1.
Der Grenzwert des Bruches im Unendlichen ist somit 1:

|
|