Unbestimmte
Ausdrücke
der Form 0·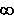 |
 |
Der unbestimmte Ausdruck  |
|
Wir betrachten nun den unbestimmten Ausdruck 0·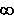 . .
Als Beispiel wählen wir den Grenzwert:

Wenn x gegen 1 geht, dann geht der erste Faktor
(die Logarithmusfunktion) gegen 0, und der zweite Faktor
(die Kotangensfunktion) geht gegen unendlich. Dies kann man
sehen, wenn man die Graphen der beiden Faktoren zeichnet:

Auf den vorigen Seiten haben wir Grenzwerte graphisch bestimmt.
Hier klappt dies nicht, denn cot(x-1) geht für (x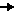 1) gegen Unendlich! 1) gegen Unendlich!
Es gibt aber einen Trick: Die Kotangensfunktion ist die Umkehrfunktion
der Tangensfunktion. Wir dürfen also den Grenzwert umformen:

Nun zeichnen wir die Zähler und Nennerfunktion, um den
Grenzwert grafisch zu ermitteln. Da Zähler- und Nennergraph
in der Nähe von x=1 gleich werden (einander anschmiegen), ist
der Quotient und somit der Grenzwert gleich 1:

|
|