Unbestimmte
Ausdrücke:
Der Fall 1 |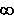
 |
Der unbestimmte Ausdruck  |
|
Zunächst wollen wir uns wieder bewußt machen,
daß der
Ausdruck 1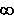
in der Potenzrechnung ein definierter Ausdruck ist,
mit dem Wert 1. Er ist also definiert und auch bestimmt (=1).
In der Grenzwertrechnung hat 1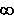 eine andere Bedeutung.
1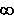
ist eine abkürzende Schreibweise für einen Grenzwert,
der an einer Stelle betrachtet wird, an der die Basis gegen 1
geht (aber nicht 1 wird), und der Exponent unendlich wird:
Beispiel:
Allgemeine Form:
Aus der Potenzrechnung wissen wir, daß eine Potenz gleich 1 ist,
wenn die Basis gleich 1 ist: 1n = 1
Wenn nun die Basis ungefähr 1 wird, kann man also vermuten,
daß die Potenz den Wert 1 hat.
Andererseits wird der Exponent unendlich groß. Potenziert man
eine Basis unendlich oft, so wird sie entweder unendlich groß
oder gleich 0.
Fazit:
Hier wirken zwei Regeln der Potenzrechnung gegeneinander,
und man kann anhand der bloßen Anschauung nicht erkennen,
welche Regel sich stärker auswirkt (also ob der Grenzwert
0 oder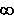
wird, oder einen Wert dazwischen annimmt).
Daher ist der Ausdruck 1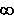 ein unbestimmter Ausdruck.
© by www.mathematik.net |
|