Version: 3
©Raddy '99

Gruppen I ZURÜCK

Assoziativität
der Verknüpfung

Vorbemerkung
      Bis jetzt waren unsere Überlegungen bis zu folgenden Punkt gelangt:
      Eine Gruppe besteht aus einer Menge und einer Verknüpfung in ihr.
      Außerdem mußte die Verknüpfung abgeschlossen sein.

      Neben der Abgeschlossenheit muß die Verknüpfung noch drei
      weitere Gesetze (Axiome) erfüllen: Die Axiome der Assoziativität,
      der Existenz eines neutralen Elementes und das Axiom der Existenz
      inverser Elemente. Diese Seite handelt vom Assoziativgesetz.

Wiederholung: Assoziativität
       Zuerst wollen wir zur Schulmathematik zurückspringen,
       und den Begriff "Assoziativität" wiederholen.
       Nehmen wir an, wir wollen drei Zahlen multiplizieren:

              3

2 =

       Nun ist es ganz egal, an welche Stellen ich eine Klammer setze,
       d.h. welche der beiden Multiplikationen ich zuerst ausführe:

              (3

2 = 30
3

2) = 30

Weil es egal ist, welche Multiplikation ich zuerst ausführe,
sagt man: Die Multiplikation ist assoziativ.

Assoziativität in unserer Beispiel-Gruppe
       Nun wollen wir auch überprüfen, ob unsere Beispiel-Gruppe
       assoziativ ist. Sie ist es, denn es gilt: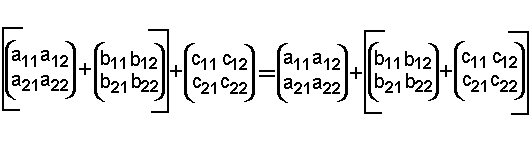
       gr1s6p1.pcx (5737 Byte)

       Beweis: Die Matrizenaddition ist elementweise definiert.
       Folglich ist die Matrizenaddition assoziativ, wenn für alle
       Matrixelemente a,b,c gilt: (a+b)+c = a+(b+c).

       Weil die Matrixelemente a,b und c reelle Zahlen sind, und
       die Addition reeller Zahlen assoziativ ist, ist auch die
       Matrixaddition assoziativ.