Version: 3 |
Gruppen I ZURÜCK |
| Existenz eines Neutralen Elementes |
 VorbemerkungAuf der Vorseite hatten wir gesagt: Die Verknüpfung R in einer Gruppe muß abgeschlossen sein und assoziativ, und es müssen neutrale und inverse Elemente vorhanden sein. Diese Seite erklärt, was ein neutrales Element ist. Wiederholung: Neutrales ElementZuerst wollen wir zur Schulmathematik zurückspringen, und den Begriff "Neutrales Element" wiederholen. Nehmen wir an, wir addieren folgende zwei Zahlen: a + 0 = a Weil man zu einer beliebigen Zahl die Zahl 0 addieren kann, ohne daß sich die Zahl a verändert, nennt man die Zahl 0 das neutrale Element der Addition. Noch ein Beispiel: Jetzt führen wir eine Multiplikation aus: a  1 = aWeil man eine beliebige Zahl a mit der Zahl 1 multiplizieren kann, ohne daß sich die Zahl a verändert, nennt man die Zahl 1 das neutrale Element der Multiplikation. Zusammengefaßt gilt: Die Null ist das neutrale Element der Addition, die Eins ist das neutrale Element der Multiplikation. Neutrales Element unserer Beispiel-GruppeNun stellt sich die Frage, wie das neutrale Element der Addition von 2x2 Matrizen lautet. Es ist eine 2x2 Matrix, die nur aus Nullen besteht. Wie wir wissen nennt man sie Nullmatrix:  Beweis: Addiert man eine 2x2 Nullmatrix zu einer beliebigen 2x2 Matrix, so bleibt die 2x2 Matrix unverändert: 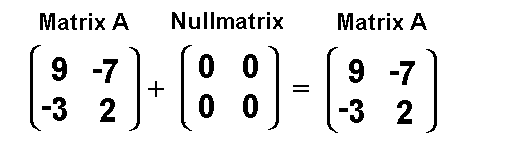 |