Version: 3 |
Gruppen I ZURÜCK |
| Existenz inverser Elemente |
 VorbemerkungAuf der Vorseite hatten wir gesagt: Die Verknüpfung in einer Gruppe muß abgeschlossen sein, und drei Gesetze erfüllen. Diese Seite erklärt das dritte Gesetz (Gesetz über die Existenz eines inverser Elemente). Wiederholung: Inverse ElementeZuerst wollen wir zur Schulmathematik zurückspringen, und den Begriff "Inverses Element" wiederholen. Nehmen wir an, wir addieren folgende zwei Zahlen: 3 + (-3) = 0 Das Ergebnis (Null) ist gleich dem neutralen Element der Addition. Deshalb nennt man die Zahl -3, das zur Zahl 3 inverse Element bezüglich der Addition. Noch ein Beispiel: Jetzt führen wir eine Multiplikation aus: 5  1/5 = 1Das Ergebnis (Eins) ist das neutrale Element der Multiplikation. Deshalb nennt man die Zahl 1/5 das zur Zahl 5 inverse Element bezüglich der Multiplikation. Inverse Elemente unserer Beispiel-GruppeNun stellt sich die Frage, wie die inversen Element bezüglich der Addition von 2x2 Matrizen heißen. Es sind die 2x2 Matrizen, deren Elemente entgegengesetzte Vorzeichen haben: 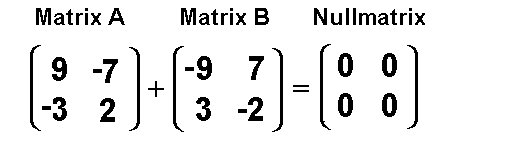 Beweis: Addiert man zur Matrix A die inverse Matrix B, so erhält man die Nullmatrix. HinweisMan beachte den Unterschied: Für die Verknüpfung in einer Gruppe gilt: Es muß nur ein neutrales Element geben, aber es muß zu jedem Element ein inverses Element geben. |