Version: 3 |
Gruppen I ZURÜCK |
| Kommutative Gruppen |
 VorbemerkungDie bis jetzt geschilderten Eigenschaften und Gesetze reichen aus, damit man von einer Gruppe reden darf. Auf dieser Seite wollen wir eine besondere Art von Gruppen kennenlernen, die sogenannten kommutative Gruppen, die auch abelsche Gruppen genannt werden (nach dem Mathematiker Niels Abel). Wiederholung: KommutativitätZuerst wollen wir zur Schulmathematik zurückspringen, und den Begriff "Kommutativität" wiederholen. Nehmen wir an, wir addieren folgende zwei natürliche Zahlen: 3 + 5 = 8 Vertauscht man die Zahlen 3 und 5, so erhält man das gleiche Ergebnis: 5 + 3 = 8 Man sagt deshalb, die Addition natürlicher Zahlen ist kommutativ. Gegenbeispiel: Die Division ist nicht kommutativ: 10 : 2 = 5 2 : 10 = 0.2 Kommutativität in unserer Beispiel-GruppeNun stellt sich die Frage, ob auch unsere Beispiel-Gruppe eine kommutative Gruppe ist. Sie ist es, denn es gilt: 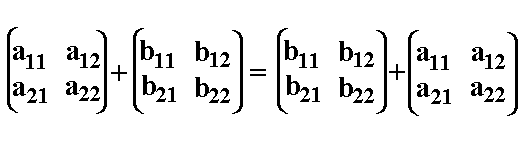 Beweis: Die Beweisidee ist die gleiche, wie beim Beweis der Assoziativität. Da die Matrixaddition komponentenweise definiert ist, braucht man nur zu beweisen: a+b = b+a für alle Elemente a, b |