Version: 3 |
Gruppen I ZURÜCK |
| Die Verknüpfung |
 VorbemerkungIn der "Definition einer Gruppe" haben wir gesagt, daß eine Gruppe aus einer Menge und einer Verknüpfung in ihr besteht. Nun wollen wir wiederholen, was eine Verknüpfung ist: Wiederholung: Was ist eine VerknüpfungEine Verknüpfung ist eine Funktion zweier Variabler. (Wir haben Verknüpfungen im Kapitel Funktionen III behandelt). Zwei Elementen wird in eindeutiger Weise ein drittes Element zugeordnet. Man schreibt: (a,b) -> c oder: a×b->c Beispiele sind z.B. 1.Die Addition natürlicher Zahlen, ganzer Zahlen, rationaler Zahlen, ... 2.Die Subtraktion natürlicher Zahlen, ganzer Zahlen, rationaler Zahlen, ... 3.Die Multiplikation natürlicher Zahlen, ganzer Zahlen, rationaler Zahlen, ... 4.Die Division natürlicher Zahlen, ganzer Zahlen, rationaler Zahlen, ... Beispiel: 3+5=8 Die Verknüpfung ist die Addition, die Zahlen 3 und 5 sind die Zahlen die verknüpft werden. Das Ergebnis der Verknüpfung ist die Zahl 8. Die Verknüpfung in unserer Beispiel-GruppeAls Verknüpfung wählen wir die Addition von 2x2 Matrizen. Zwei 2x2-Matrizen wir durch die Verknüpfung (Addition) eine dritte 2x2-Matrix zugeordnet. Wie wir wissen (Matrizen II) ist die Addition von Matrizen komponentenweise definiert: 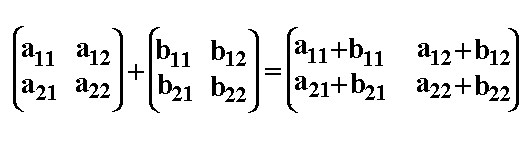 |