Version: Test
©Raddy 2000

Inhalt zu: Gruppen II                               ZURÜCK
Info-Seite Notwendige Vorkenntnisse: Gruppen I
Thema des Kapitels: Weiteres Beispiel für eine Gruppe
Infos: www.mathematik.net
Die Menge
(Beispiel)		 Eine Gruppe besteht ja grob gesagt aus einer Menge und einer
Verknüpfung. In diesem Kapitel betrachten wir eine Gruppe,
die auf folgender Menge konstruiert wird: Die Menge der Drehungen
eines Quadrates um den Winkel 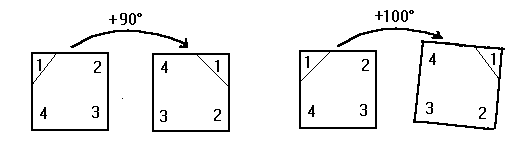a-g-alpa.pcx (200 Byte)m-elem.pcx (209 Byte)R (R=reelle Zahl). Zwei Beispiele:
gr1s0p2.pcx (4485 Byte)
Die Verknüpfung

 Eine Verknüpfung in dieser Menge ist die "Addition von Drehungen"
im Sinne von einer "Hintereinander-Ausführung zweier"
Drehungen. Die Verknüpfung schreibt sich somit:

                                Drehung 1 + Drehung 2
 
Abgeschlossenheit
der Verknüpfung		 Zwei Drehungen der Menge G ergeben wieder eine Drehung
der Menge G. Unsere Verknüpfung ist also abgeschlossen
Assoziativität Die Verknüpfung dreier Drehungen ist assoziativ.
Neutrales
Element		 Das neutrale Element ist eine Drehung um 0°.
Inverse
Elemente		 Die inversen Elemente sind Drehungen mit umgekehrten
Vorzeichen, also Drehungen in die umgekehrte Richtung.
Kommutative
Gruppen		 Die Hintereinander-Ausführung zweier Drehungen ist kommutativ.