Version: Test |
Gruppen II ZURÜCK |
| Die Verknüpfung |
 VorwortWie schon öfter erwähnt besteht eine Gruppe aus einer Menge und einer Verknüpfung auf dieser Menge. Eine Menge haben wir auf der vorigen Seite ausgewählt, nun müssen wir eine Verknüpfung in ihr definieren: Verknüpfung in unserem BeispielAuf der vorigen Seite hatten wir die Menge G betrachtet: Die Menge aller Drehungen eines Quadrates um seine Achse Nehmen wir nun zwei Elemente dieser Menge, z.B. die beiden Elemente "Drehung um +90°" und "Drehung um +180°", und führen diese beiden Drehungen hintereinander aus, so entspricht dies einer Drehung um +270°: 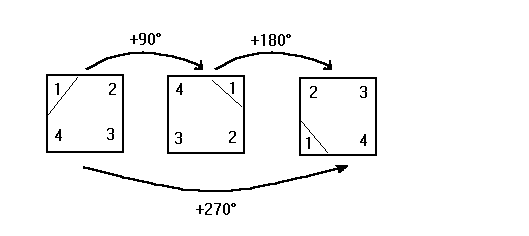 Die Verknüpfung in unserem Beispiel ist wieder eine Addition, so wie im Kapitel Gruppen I, als wir Matrizen addiert haben. Allerdings werden in diesem Beispiel keine Matrizen addiert, sondern eben Drehungen. |