Version: Test ©Raddy 2000	Inhalt zu: Gruppen III ZURÜCK
Info-Seite	Notwendige Vorkenntnisse: Gruppen I Thema des Kapitels: Weiteres Beispiel für eine Gruppe Infos: www.mathematik.net
Die Menge (Beispiel)	Eine Gruppe besteht ja grob gesagt aus einer Menge und einer Verknüpfung. In diesem Kapitel betrachten wir eine Gruppe, die auf folgender Menge konstruiert wird: Die Menge der (euklidischen) Vektoren der Ebene. Bild: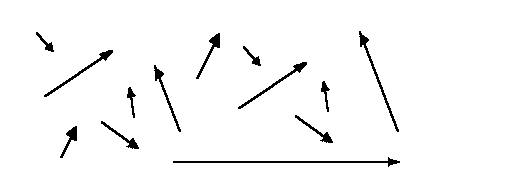
Die Verknüpfung	Als Verknüpfung wählen wir die Addition zweier euklidischer Vektoren der Ebene. Diese Verknüpfung kennen wir bereits aus der Schule, oder aus dem Kurs Vektoralgebra: Man addiert zwei Vektoren a und b, indem man den Anfang des Vektors b an das Ende des Vektors a verschiebt. Der Vektor a+b ist dann der Vektor, der vom Anfang vom a bis zum Ende von b reicht.
Abgeschlossenheit der Verknüpfung	Addiert man zwei Vektoren der Ebene, so ist das Ergebnis wieder ein Vektor der Ebene. Unsere Verknüpfung ist also abgeschlossen
Assoziativität	Die Addition dreier Vektoren der Ebene ist assoziativ.
Neutrales Element	Das neutrale Element ist der Nullvektor.
Inverse Elemente	Die inversen Elemente sind Vektoren mit umgekehrter Richtung.
Kommutative Gruppen	Die Vektoraddition zweier Vektoren der Ebene ist kommutativ. Dies sieht man am sogenannten Kräfteparallelogramm.