Version: Test |
Gruppen III ZURÜCK |
| Die Verknüpfung |
Wie schon öfter erwähnt besteht eine Gruppe aus einer Menge und einer Verknüpfung auf dieser Menge. Eine Menge haben wir auf der vorigen Seite ausgewählt, nun müssen wir eine Verknüpfung in ihr definieren: Auf der vorigen Seite hatten wir die Menge G betrachtet: Menge der euklidischen Vektoren der Ebene Als Verknüpfung wählen wir nun die Vektoraddition, die wir aus der Vektorrechnung (Kurs: Vektoralgebra I) kennen:
|
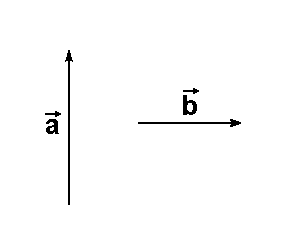 Gegeben seien die beiden
Vektoren
Gegeben seien die beiden
Vektoren 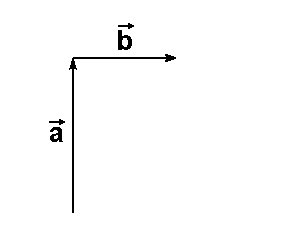 Nun ersetzen wir den gegebenen
Repräsentanten des Vektors
Nun ersetzen wir den gegebenen
Repräsentanten des Vektors 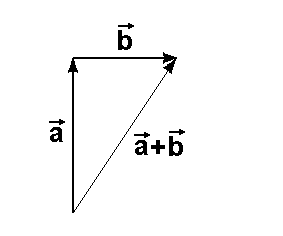 Der Vektor
Der Vektor