|
Die Divergenz der harmonische Reihe wurde 1689 von Jakob Bernoulli
nachgewiesen.
Der Beweis beruht darauf, dass ich eine Reihe nehme, von der ich weiß,
dass sie kleiner als die harmonische Reihe ist. Dann beweise ich, dass
auch die
kleinere Reihe divergiert, und somit automatisch auch die größere, also
die harmonische Reihe.
Die harmonische Reihe lautet:
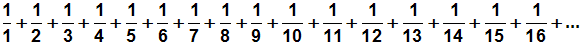
Wir beginnen bei 1/3 und fassen 2, 4, 8, 16, 32, 64, ....
Summanden zusammen.
Man beachte, dass man unendlich viele Gruppen bilden kann:
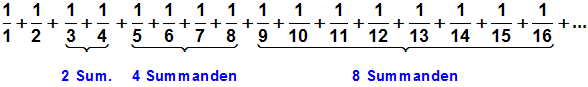
| Die Gruppe mit 2 Summenden ist größer als
y
,denn es gilt: |
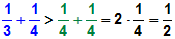 |
| Die Gruppe mit 4 Summenden ist größer als
y
,denn es gilt: |
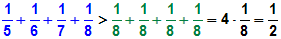 |
| Die Gruppe mit 8 Summenden ist größer als
y
,denn es gilt: |
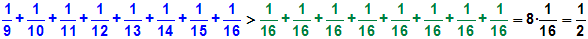 |
Wir können also schreiben:
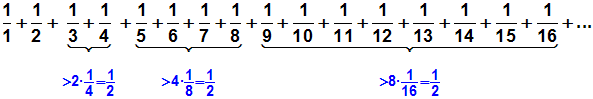
Anscheinend ist jeder dieser Gruppen größer als 1/2, also zumindest so
groß wie 1/2.
Und da man
unendlich viele Gruppen
bilden kann, die so groß sind wie 1/2,
wird der Wert der Reihe unendlich groß, d.h. sie
divergiert, was zu beweisen war. |