Die lineare Funktion
f(x)=mx |
 |
Der Funktionsgraph der
linearen Funktion f(x)=mx |
|
In diesem Kapitel geht es erstmal um lineare Funktionen der Form f(x)=m·x,
also zum Beispiel um die Funktion:
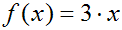
Dabei nennt man x die unabhängige Variable, weil man für x
beliebige
Zahlen einsetzen kann. Wenn man für x eine Zahl einsetzt, dann erhält
man den Funktionswert f(x).
Manchmal gibt man dem Funktionswert f(x) den Namen y.
Man sagt:
Dem Funktionswert wird die abhängige Variable y
zugeordnet.
Anstatt f(x)=3x schreibt man dann y=3x.
Zuerst wollen wir zeigen, wie man den Funktionsgraphen dieser
Funktion zeichnet. Dazu stellen wir eine Wertetabelle auf.
Um die Wertetabelle aufzustellen, wählen wir verschiedene Zahlen für x,
und tragen sie in eine Tabelle ein, zum Beispiel die Zahlen 1,2,3,4 und
5:
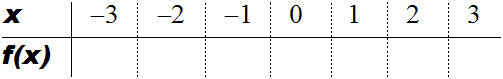
Jetzt setzen wir diese Zahlen (x-Werte) nacheinander in die Funktion
f(x)=3·x ein
und berechnen, welche Funktionswerte f(x) entstehen. Setzen wir zum Beispiel
für x die Zahl –3 ein, dann erhalten wir: f(x)=3·(–3)=
–9
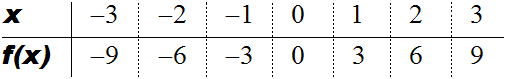
Diese Punkte tragen wir jetzt in ein Koordinatensystem ein.
Zum Beispiel ergibt x= –3 den Punkt (–3/–9).
Dadurch
erhalten wir den Funktiongraphen der linearen Funktion:
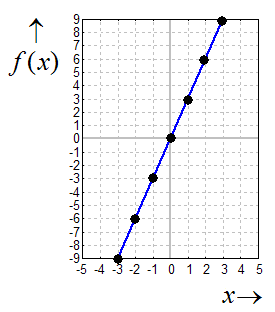
Wie man sieht erhält man eine gerade Linie, und daher bezeichnet man die
Funktion als "lineare Funktion". Manchmal wird die "lineare Funktion"
auch als "Proportionalität" bezeichnet. |
| |
|