Die
Zwei-Punkte-Formel
der Steigung |
 |
Worum geht es |
|
Auf der vorigen Seite haben wir die Steigung m am Funktionsgraphen
abgelesen. Nun wollen wir erklären, wie man die Steigung m rechnerisch
ermitteln kann. Dazu lernen wir die Zwei-Punkte-Formel kennen.
|
 |
Die Zwei-Punkte-Formel |
|
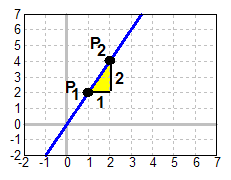
Wir wiederholen zunächst, wie wir auf der vorigen Seite die
Steigung m berechnet haben: Wir sind vom Punkt P1 um eine Einheit auf
der x-Achse nach rechts gegangen, und haben überprüft, um
wieviel sich dabei der y-Wert änderte. Wir haben also die
y-Änderung pro x-Änderung berechnet:
 |
 |
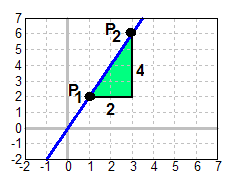
Wir hätten auch ein größeres Steigungsdreieck einzeichnen
können. Wir hätten zum Beispiel vom Punkt P1 um
zwei Einheiten nach
rechts gehen können, und dann die Änderung des y-Wertes
bestimmen können.
 |
 |
Nun versuchen wir die y-Änderung durch die Koordinaten der
Punkte auszudrücken.
Der Punkt P1 hat die y-Koordinate y1= 2,
der Punkt P2 hat die y2-Koordinate 6.
Die y-Änderung ist also die y-Koordinate von P2 minus
der y-Koordinate von P1:
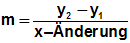
Der Punkt P1 hat die x-Koordinate x1=1,
der Punkt P2 hat die x-Koordinate x2=3.
Die x-Änderung ist gleich der x-Koordinate von P2
minus der x-Koordinate von P1:
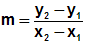
Diese Formel nennt sich "Zwei-Punkt-Formel" weil wir die
Steigung
berechnen können, wenn zwei Punkte gegeben sind. |
|
| |
|