Ein Punkt ist gegeben:
Berechnung der Funktionsgleichung |
 |
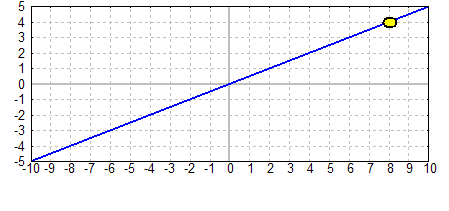
Funktionsgraph |
|
 |
 |
Gegeben und gesucht |
|
Wir nehmen nun an, dass von einer linearen Funktionen der Form f(x)=m·x
ein Punkt gegeben sei, z.B. der Punkt (8/4).
Gesucht ist die Funktionsgleichung.
|
 |
Lösungsweg |
|
Wir wissen, dass die Funktion die Form f(x)=m·x haben soll. Daher kennen
wir einen zweiten Punkt, denn alle linearen Funktionen der Form f(x)=m·x
gehen durch den Punkt (0/0), wie wir auf der vorigen Seite gelernt
haben.
Da uns also zwei Punkte bekannt sind, können wir die Zwei-Punkte-Formel
anwenden, die wir auf den vorigen Seiten kennengelernt haben:
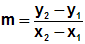
In diese Formel setzen wir die Koordinaten der beiden gegebenen Punkte
ein,
also die Koordinaten (0/0) und (8/4). Dann berechnen wir den Wert des
Bruches:
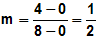
Die Steigung der Funktion beträgt also m=1/2, oder anders geschrieben:
m=0.5.
Die gesuchte Funktionsgleichung lautet also:
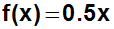 |
| |
|