Die lineare Funktion
f(x)=m·x+a |
 |
Vorbemerkung |
|
Wir behandeln jetzt die Funktion f(x)=m·x+a. Obwohl sie eigentlich
eine sogenannte affine Funktion ist, werden wir sie als
lineare Funktion
bezeichnen, weil dies in der Schule so üblich ist.

|
 |
Erklärung |
|
Im vorigen Kapitel haben wir lineare Funktionen der Form
f(x)=m·x
behandelt. Jetzt geht es um lineare Funktionen der Form
f(x)=m·x+a.
Wie man sieht wird bei den zuletztgenannten Funktionen eine Konstante
(konstante Zahl) a zum Funktionsterm hinzuaddiert. Dadurch verschiebt
sich der Funktionswert um a Einheiten nach oben.
Als Beispiel wählen wir die Funktionen f(x)=2x und f(x)=2x+3:
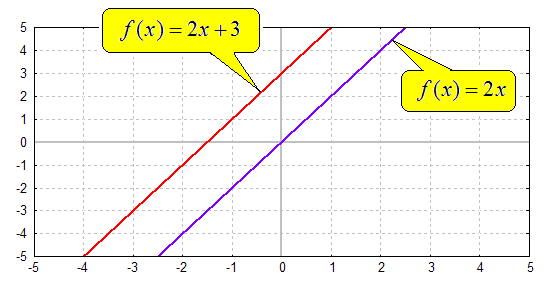
Wie man sieht bewirkt die "3", dass der Funktionsgraph um 3 Einheiten
nach
oben verschoben wird.
Wenn a negativ ist, also zum Beispiel bei f(x)=2x–5, dann wird der
Funktionsgraph
um a Einheiten nach unten verschoben, also im Beispiel um 5 Einheiten. |
| |
|