 |
Überblick |
|
Auf dieser Seite lernen wir das folgende:
Eine Balkenwaage bleibt also im Gleichgewicht, wenn man auf
beiden Seiten
das gleiche Gewicht hinzufügt, abzieht oder die Anzahl der
Gewichte
mit einer Zahl multipliziert oder durch eine Zahl dividiert. |
. |
 |
1. Addieren von Gewichten |
|
Wir betrachten nun eine Balkenwaage. So eine Balkenwaage wird zum
Wiegen benutzt. Sie funktioniert genauso wie eine Wippe auf dem
Spielplatz.
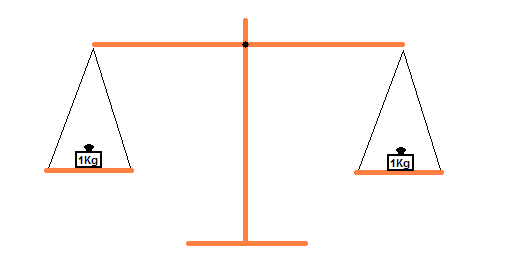
Die Balkenwaage ist im Gleichgewicht, wenn auf beiden
Seiten des Balkens
das gleiche Gewicht hängt, zum Beispiel wenn auf
beiden Seiten der Waage
1Kilogramm (1Kg) hängt:
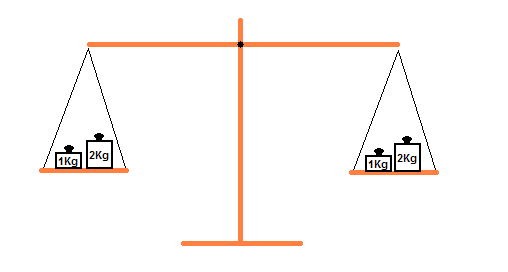
Jetzt legen wir auf beide Waageschalen ein zusätzliches Gewicht
von 2Kg.
Die Waage wird im Gleichgewicht bleiben, weil wir auf beiden Seiten das
gleiche Gewicht addiert haben:
|
 |
2.Subtrahieren von Gewichten |
|
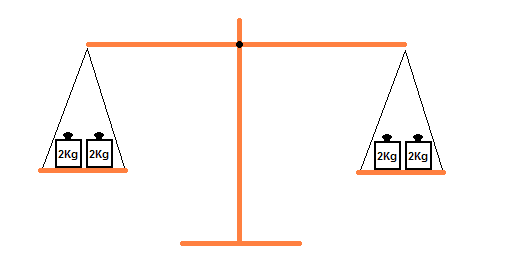
Jetzt nehmen wir an, auf
beiden Seiten der Waage würden 4 Kilogramm hängen:
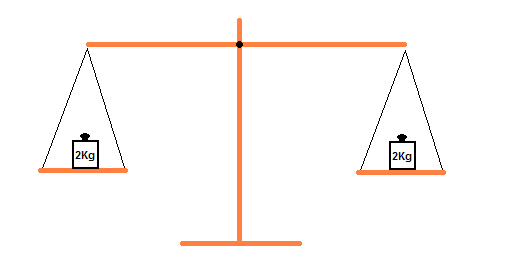
Jetzt nehmen wir aus beiden Waagschalen ein 2Kg Gewicht heraus, das
heißt
wir ziehen auf beiden Seiten das gleiche Gewicht ab. Auch
dann wir die Waage
im Gleichgewicht bleiben:
 |
 |
3.Multiplizieren
der Anzahl der Gewichte |
|
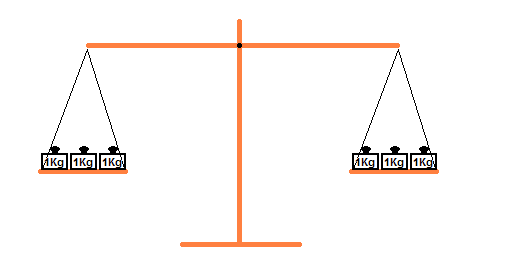
Als Beispiel nehmen wir an, auf beiden Waageschalen würde
wieder je 1 Kg liegen:

Jetzt legen wir auf beiden Waagschalen die dreifache Menge an
Gewichten,
das heißt wir multiplizieren auf beiden Seiten die Anzahl der
Gewichte mit der
gleichen Zahl. Auch in diesem Fall bleibt die Waage im
Gleichgewicht:
|
 |
4.Dividieren der Anzahl der Gewichte |
|
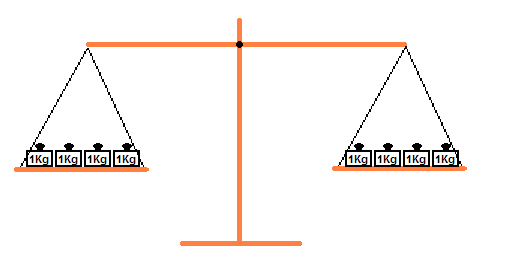
Als Beispiel nehmen wir an, auf beiden Waageschalen würden 4 Kg liegen:
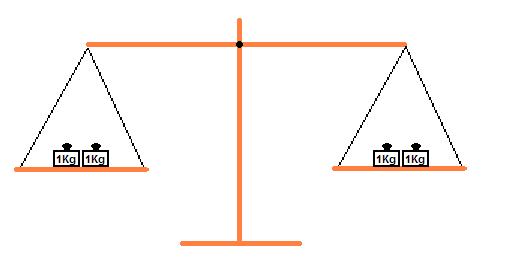
Jetzt halbieren wir die Anzahl Gewichte auf beiden Seiten, das heißt wir
dividieren
auf beiden Seiten die Anzahl der Gewichte durch die gleiche
Zahl, nämlich durch
die Zahl 2. Auch in diesem Fall bleibt die Waage im Gleichgewicht:
|
| |