Lineare Gleichungen
der Form: a·x=b |
 |
1. Die lineare Gleichung: a·x=b |
|
Wir betrachten jetzt lineare Gleichungen, bei denen x in einem
Produkt vorkommt, d.h. vor dem x steht ein Faktor (eine Zahl):
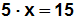
Wir haben gesagt, dass man eine Gleichung löst, indem man x auf einer
Seite isoliert (isolieren bedeutet, x muß allein auf einer Seite
stehen).
Um x zu isolieren, müssen wir die "5" auf die andere Seite der Gleichung
bringen. Dazu müssen die "umgekehrte Rechenoperation" auf die 5
anwenden. Das bedeutet: Weil die 5 mit x multipliziert wird,
müssen wir die Gleichung
durch die Zahl 5 dividieren:
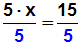
Den Bruch auf der linken Seite der Gleichung kann man mit 5 kürzen:
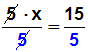
Auf der linken Seite bleibt x übrig, und die rechte Seite kann man
ausrechnen:
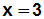
Die Lösung ist x=3.
|
 |
2. Die lineare Gleichung: x·a=b |
|
Das folgende Beispiel ähnelt dem vorigen Beispiel, doch diesmal
steht die Zahl nicht vor dem x, sondern hinter dem x:
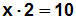
Wir haben gesagt, dass man eine Gleichung löst, indem man x auf einer
Seite isoliert (isolieren bedeutet, x muß allein auf einer Seite
stehen).
Damit x allein auf einer Seite steht, müssen wir beide Seiten der
Gleichung
durch die Zahl 2 dividieren, also durch die Zahl, die hinter dem x
steht:
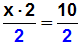
Den Bruch auf der linken Seite der Gleichung kann man mit 2 kürzen:
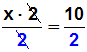
Auf der linken Seite bleibt x übrig, und die rechte Seite kann man
ausrechnen:
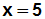
Die Lösung ist x=5.
|
| |
|