Lineare Gleichungen
der Form: x:a+b=c |
 |
Lineare Gleichungen der Form: x:a+b=c |
|
Wir betrachten wieder eine lineare Gleichung mit zwei
Rechenzeichen,
aber diesmal mit einer Division statt einer Multiplikation:
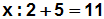
Zuerst müssen wir die "5" von der linken Seite der Gleichung auf
die rechte Seite bringen. Weil die auf der linken Seite "5" addiert
wird,
müssen wir auf beiden Seiten der Gleichung die "5" subtrahieren,
denn man muß ja immer die umgekehrte Rechenoperation wählen:
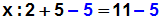
Auf der linken Seite heben sich +5 und –5 gegenseitig auf. Auf der
rechten Seite können wir 11–5 ausrechnen, und erhalten 6:
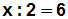
Als nächstes beseitigen wir die Punktrechnung, also die Division durch
2.
Weil die Umkehrung der Division die Multiplikation ist, müssen wir
beiden Seiten der Gleichung mit 2 multiplizieren:
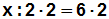
Auf der linken Seite der Gleichung heben sich die Division durch 2
und die Multiplikation gegenseitig auf, auf der rechten Seite der
Gleichung können wir 6·2 ausrechnen, und erhalten 12:
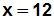
Das Ergebnis lautet also x=12. |
| |
|