Für Basis>1 gilt:
Je größer die Basis
desto flacher der Graph |
 |
Das Beispiel |
|
Nun betrachten wir
Logarithmusfunktionen mit verschiedener Basis,
wobei die Basis größer 1 sein soll:
f(x)=logbx mit: b>1
Im Beispiel vergleichen wir die Funktionen f(x)=log2(x) und f(x)=log5(x):
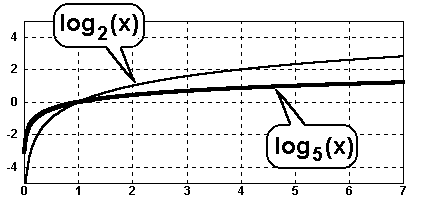
|
 |
Verlauf für x>1 |
|
Die Logarithmusfunktion mit der
Basis 2 verläuft oberhalb der
Logarithmusfunktion mit der Basis 5. Eine Logarithmusfunktion
mit kleiner Basis wächst also schneller gegen +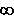 . .
Wie kann das herausfinden, ohne die Funktionen zu zeichen? Ja!
Dazu schreiben wir die Funktion in der äquivalenten Potenzschreibweise:
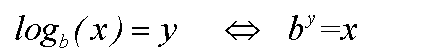
Nun betrachen wir eine bestimmte Stelle x, und dadurch wird by=konstant:
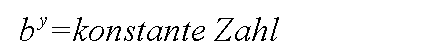
Wenn die Basis b in der Gleichung klein ist, muß der Funktionswert y groß sein.
Eine Logarithmusfunktion mit kleiner Basis b (b>1) hat also einen großen Funktionswert
y. |
 |
Verlauf für 0<x<1 |
|
Die Logarithmusfunktionen mit der
Basis 2 verläuft nun unterhalb der
Logarithmusfunktionen mit der Basis 5, und geht daher schneller gegen –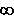 . . |
|