Streng monoton
fallend, wenn für
die Basis gilt:
0<a<1 |
 |
Monotonie der Logarithmusfunktion |
|
Wenn die Basis a zwischen Null und
Eins liegt (0<a<1),
dann ist die Logarithmusfunktion streng monoton fallend, d.h.
die Funktionswerte nehmen von links nach rechts beständig ab.
Die Funktionswerte nehmen von links nach rechts nicht nur ständig ab,
die Funktionswerte gehen sogar gegen – 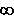 (Minus
Unendlich).
(Beachte: Nicht jede streng monoton fallende Funktion geht auch automatisch
gegen – 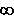, sie könnte auch konvergieren, mehr im Kurs Grenzwerte).
Je mehr man sich dagegen der Stelle x=0 nähert, desto mehr schmiegt sich
der Graph der Funktion an die y-Achse an. Man sagt, die y-Achse ist eine
vertikale Asymptote der Funktion. Die Funktionswerte gehen dabei
gegen + :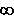
 |
|
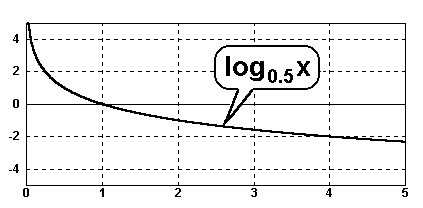