Für Basis 0<b<1 gilt:
Je größer die Basis
desto steiler der Graph |
 |
Das Beispiel |
|
Nun betrachten wir
Logarithmusfunktionen mit verschiedener Basis,
wobei die Basen zwischen 0 und 1 liegen sollen:
f(x)=logbx mit: 0<b<1
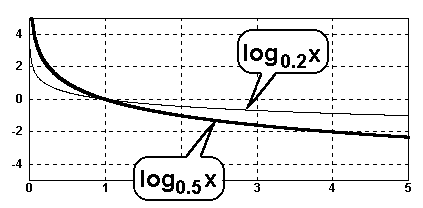
Im Beispiel vergleichen wir die Funktionen f(x)=log 0.5(x) und f(x)=log
0.2(x):
 |
 |
Verlauf für x>1 |
|
Die Logarithmusfunktion mit der
Basis 0.5 verläuft unterhalb der
Logarithmusfunktion mit der Basis 0.2. Eine Logarithmusfunktion
mit größerer Basis fällt also schneller gegen –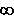 . . |
 |
Verlauf für 0<x<1 |
|
Die Logarithmusfunktionen mit der
Basis 0.5 verläuft nun oberhalb der
Logarithmusfunktionen mit der Basis 0.2, und geht daher schneller gegen +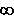 , ,
wenn man sich der Stelle x=0 nähert. |
|