Spiegelung des
Graphen an der
y-Achse
|
 |
Erklärung |
|
Gegeben sei eine Logarithmusfunktion
f(x):
f(x) = logb(x)
Beispiel: log2(x)
Wenn wir dem Numerus ein negatives Vorzeichen geben:
g(x) = logb(–x)
Beispiel: log2(–x)
dann entsteht eine Funktion g(x) deren Graph spiegelbildlich zum Graphen
der Funktion f(x) liegt, und zwar spiegelbildlich bezüglich der y-Achse.
Beachte: Der Definitionsbereich der neuen Funktion g(x) ist R < 0 |
|
 |
Erklärung zum Definitionsbereich |
|
Wie gesagt ist besteht der
Definitionsbereich nun nur noch aus den negativen
reellen Zahlen, d.h. wir dürfen für x nur negative Zahlen einsetzen.
Als Beispiel setzen wir –8 in das obige Beispiel g(x)=log2(–x) ein:
g(–8) = log2(–(–8))
= log2(8)= 3
Würde man nämlich positive Zahlen für x
einsetzen, dann wäre der
Numerus negativ. Logarithmen mit negativen Numerus sind aber nicht definiert:
g(8) = log2(–8) = nicht definiert |
 |
Beispiel |
|
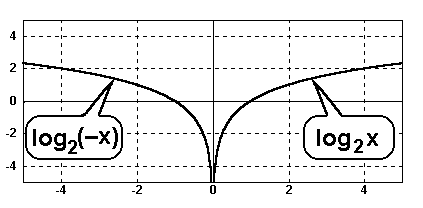
Als Beispiel betrachten wir wieder die beiden Beispiel-Funktionen:
f(x)=log2x
und g(x) = log2(–x)
Die beiden Funktionen liegen spiegelbildlich zur y-Achse, haben
aber (wie breits gesagt) unterschiedliche Definitionsbereiche.
|
|