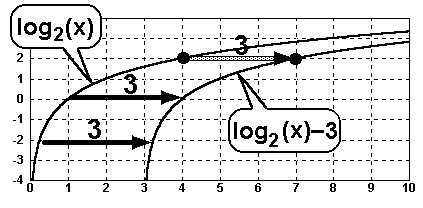Wird zum Numerus nun eine Konstante k>0 subtrahiert:
g(x)=logb(x–k)
Beispiel: g(x)=log2(x–3)
so entsteht ein Graph, der gegenüber den ursprünglichen Funktionsgraphen um die
Konstante Zahl k in Richtung der x-Achse nach rechts verschoben ist.
Bild und Erklärung
Als Beispiel betrachten wir die Funktionen im Bild oben:
f(x)= log2(x) und g(x)= log2(x–3)
und den Funktionswert y=2. Der Funktionswert y=2 wird im Falle
der Allgemeinen Logarithmusfunktion log2(x) bei x=4 erreicht, bei der
verschobenen Logarithmusfunktion log2(x–3) aber erst bei x=7.
Die Allgemeinen Logarithmusfunktion f(x)=log2(x) muß also um 3 Einheiten
nach rechts verschoben werden, um die Funktion g(x)=log2(x–3) zu erhalten.
Als Beispiel betrachten wir die Funktionen im Bild oben:
f(x)= log2(x) und g(x)= log2(x–3)
und den Funktionswert y=2. Der Funktionswert y=2 wird im Falle
der Allgemeinen Logarithmusfunktion log2(x) bei x=4 erreicht, bei der
verschobenen Logarithmusfunktion log2(x–3) aber erst bei x=7.
Die Allgemeinen Logarithmusfunktion f(x)=log2(x) muß also um 3 Einheiten
nach rechts verschoben werden, um die Funktion g(x)=log2(x–3) zu erhalten.