| Streckung in Richtung der x-Achse |
 |
Satz |
|
Gegeben sei die Allgemeine
Logarithmusfunktion:
f(x)=logbx
Beispiel: f(x)=log2x
Wird der Numerus mit dem Faktor 0<n<1 multipliziert:
g(x)=logb(n·x)
Beispiel: g(x)=log2(0.5·x)
so entsteht ein Graph, der gegenüber den ursprünglichen Funktionsgraphen
auf das 1/n-fache in Richtung der x-Achse gestreckt ist. |
|
|
Bild und Erklärung |
|
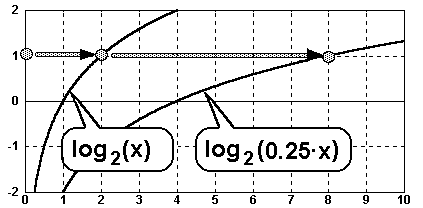Als Beispiel betrachten wir die Funktionen im Bild oben:
f(x)= log2x und g(x)= log2(0.25·x)
Die Funktion g(x)=log2(0.25·x) erreicht einen bestimmten Funktionswert
(z.B. y=1) zu einem viermal späteren Zeitpunkt als die Funktion f(x). Die Funktion
g(x) erscheint um den Faktor 4 in Richtung der x-Achse gestreckt.
© www.mathematik.net |
|