In diesem Kapitel betrachten wir die einfachsten aller Logarithmusgleichungen.
Sie bestehen aus nur einem Logarithmus und einem Absolutglied (hier: 2):
  
     
  
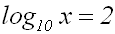
Wir wollen diese Gleichung lösen, d.h. wir wollen die Gleichung nach x umstellen.
Dazu brauchen wir uns nur an die Definition des Logarithmus erinnern, die wir im
Kurs Logarithmen kennengelernt haben: Der Logarithmus ist ein Exponent. Genauer:

Der Logarithmus (2) ist der Exponent, mit dem man die Logarithmusbasis (10)
potenzieren muß, um den Numerus (x) zu erhalten:


     

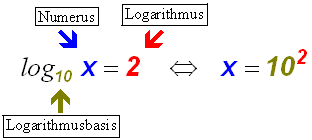
Damit haben wir die Logarithmusgleichung gelöst:
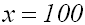