Das Problem:

Im vorigen Kapitel haben wir Logarithmusgleichungen betrachtet, die aus zwei Logarithmen bestanden.
Solche Gleichungen löst man durch das Lösungsverfahren "Vergleich der Numeri". Oft stört ein Faktor
vor einem (oder vor beiden) Logarithmen:, denn dann können wir das Verfahren nicht anwenden:

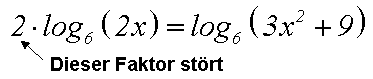
Daher brauchen wir eine Methode, wie man einen "Faktor vor dem Logarithmus" beseitigen kann.
  

Das Lösungsverfahren:

Um einen Faktor zu beseitigen, der vor einem Logarithmus steht, muss man das 3.Logarithmusgesetz anwenden.

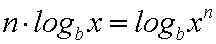
Beim Anwenden des 3.Logarithmusgesetzes in der Leserichtung "von links nach rechts" können
Lösungen hinzukommen, d.h. wir dürfen die Probe nicht vergessen. Allerdings haben wir ja bereits erwähnt,
dass wir die Probe beim Lösen von Logarithmusgleichungen grundsätzlich machen wollen.
    

Beispiel:

Gegeben ist wieder die Gleichung von ganz oben:

Wir wenden das 3.Logarithmusgesetz auf die linke Seite der Logarithmusgleichung an:

Jetzt können wir das Lösungsverfahren aus dem vorigen Kapitel
anwenden, d.h. wir müssen die Numeri gleichsetzen:

Die linke Seite können wir mit Hilfe der Potenzrechnung vereinfachen:

Wir subtrahieren 3x² auf beiden Seiten:

Potenzgleichung lösen ergibt:
    
Die Probe ergibt, dass nur +3 eine Lösung ist, denn x = –3 führt
zu einen undefinierten Logarithmus (wegen negativen Numerus):