Nun betrachten wir die Logarithmusgleichung:
  
     
  
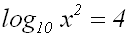
Um die Gleichung zu lösen, benutzen wir wieder die Definition des Logarithmus:

Der Logarithmus (4) ist der Exponent, mit dem man die Logarithmusbasis (10)
potenzieren muß, um den Numerus (x) zu erhalten:
  
       
  
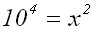
Wir rechnen die linke Seite aus:
  
    
  
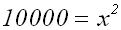
Wir lösen die Potenzgleichung, indem wir auf beiden Seiten die Wurzel ziehen:
  
    
  
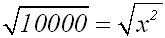
Es ergibt sich die Gleichung:
  
    
  
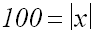
Die Lösungen dieser Betragleichung bzw. der Logarithmusgleichung lauten:
  
     
  
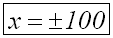
Wir machen noch die Probe, indem wir beide Lösungen in die ursprüngliche
Gleichung einsetzen. Wir erkennen, daß beide Lösungen richtig sind.