Beispiel:

Wir betrachten nochmals die gleiche Logarithmusgleichung,
die wir zu Beginn dieses Kapitels gelöst haben:
     

Beweis des Verfahren (kann übersprungen werden):

Wir müssen klären, ob man beide Seiten einer Gleichung in den Exponenten erheben darf,
ohne daß sich die Lösungsmenge ändert, also ob dies eine Äquivalenzumformung ist.
Zur Klärung dieser Frage betrachten wir die folgende Formel:
           
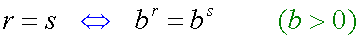
Die Formel sagt, daß man zwei Zahlen oder Terme (r und s) in den Exponenten
erheben kann, ohne daß sich die Lösungsmenge ändert.

Nun müssen wir die Formel beweisen:.

Leserichtung links nach rechts:
Für die Exponentialfunktion gilt das gleiche, wie für alle Funktionen:
Zu einem bestimmten Wert gibt es genau einen Funktionswert.
bestimmten Wert r=s genau einen Funktionswert b^r=b^s

Leserichtung rechts nach links:
Das man die Formel von rechts nach links richtig ist liegt daran, daß die Exponentialfunktion
streng monoton steigend ist: Zu einem bestimmten Funktionswert b^r=b^s gibt es genau
einen Wert, d.h. es gilt r=s