Wir betrachten eine Logarithmusgleichung, bei welcher der Numerus eine Potenz ist:

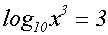
Man könnte sie auch durch direkte Anwendung des Lösungsverfahren aus Kapitel 1 lösen,
d.h durch Anwenden der Definiton des Logarithmus. Uns geht es aber darum, die Anwendung
des 3.Logarithmusgesetzes zu untersuchen, und zwar die Leserichtung "von rechts nach links".

Zur Erinnerung ist hier nochmal das 3.Logarithmusgesetz aufgeführt: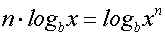 

Wir wenden das 3.Logarithmusgesetz "von rechts nach links" an, und erhalten:

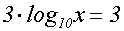
Wir teilen beide Seiten durch 3:

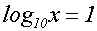
Jetzt wenden wir die "Definition des Logarithmus" aus Kapitel 1 an:

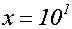
Wir vereinfachen:

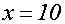
Die Probe ergibt, dass x=10 wirklich eine Lösung der Logarithmusgleichung ist.

Auf der nächsten Seite zeigen wir, dass die Anwendung der
Leserichtung von rechts nach links (beim 3.Logarithmusgesetz)
nicht immer so unproblematisch ist.
Ist der Exponent im Numerus nämlich eine gerade Zahl,
dann können Lösungen verlorengehen!