Beweis des Verfahrens:

Zum Beweis betrachten wir eine Logarithmusgleichung mit zwei Logarithmen.
Die Numeri sind von x abhängige Terme: 
Beispiel:
Nun wenden wir die "Definition des Logarithmus" ,
die wir im Kapitel 1 bereits kennengelernt haben, auf die linke Seite der Gleichung an:
Beispiel:
Auf der linken Seite heben sich Logarithmieren und Potenzieren auf, weil die Exponentialfunktion
die Umkehrfunktion der Logarithmusfunktion ist:
Beispiel:
Damit ist das Lösungsverfahren (fast) bewiesen.Wir müssen nämlich noch beweisen,
dass eine Probe notwendig ist.
   

Beweis der Notwendigkeit der Probe:

Betrachten wir dazu die erste Umformung, d.h. die erste Anwendung der Defintion des Logarithmus:
Vor der Umformung besteht der Defintionsbereich von f(x) nur aus den positiven reellen Zahlen,
denn Logarithmen sind nur für positive Zahlen definiert, doch nach der Umformung besteht der
Definitionsbereich von f(x) aus allen reellen Zahlen.

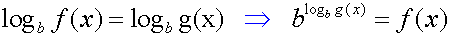
Das gleiche passiert nochmals bei der zweiten Umformung, doch diesmal
vergrößert sich der Definitionsbereich von g(x):

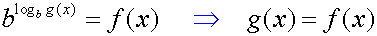
Durch die Vergrößerung des Defintionsbereiches können auch Lösungen hinzukommen,
falls diese im neuen, erweiterten Teil des Definitionsbereich liegen. Daher ist die Probe nötig.