|
|
Um Logarithmusgleichungen mit zwei Logarithmen zu lösen,
brauchen wir den folgenden Satz: |
Wenn zwei Logarithmen (mit gleicher Basis b) gleich sind, dann sind
auch ihre Numeri gleich:
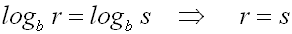 |
Für Interessierte beweisen wir den
Satz am Ende des Kapitels
|
|
Anwendung auf
Logarithmusgleichung: |
Wichtig: Die Probe ist immer
nötig |
Bei Anwendung des Satzes können Lösungen
hinzukommen. Wir müssen daher immer die Probe machen.
Vereinbarung: Weil bei fast allen Lösungsverfahren für Logarithmusgleichungen eine
Probe nötig ist,
werden wir ab jetzt immer eine Probe machen, wenn wir eine Logarithmusgleichung lösen. |
|
|