Das Problem

Bis jetzt haben wir Logarithmusgleichungen betrachtet, die ein oder zwei Logarithmen bestanden.
Kommt zusätzlich noch ein weiteres Glied hinzu, z.B. ein Absolutglied (hier die Zahl 2 bzw. 3),
dann versagen die Lösungsverfahren, die wir bisher kennengelernt haben:
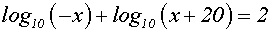              Beispiel (1)
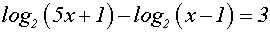             Beispiel (2)  
              

Die Lösungsmethode:

Um solche Gleichungen zu lösen, brauchen wir das 1.und 2.Logarithmusgesetz.
Die Lösungsidee besteht darin, dass man die Logarithmen mit Hilfe des
1. bzw. 2.Logarithmusgesetzes zu einen einzelnen Logarithmus zusammenfasst.
     1.Logarithmusgesetz
          2.Logarithmusgesetz

Im Beispiel (1) können wir die Logarithmen mit Hilfe des 1.Logrithmusgesetzes zusammenfassen:

Im Beispiel (2) müssen wir das 2.Logrithmusgesetz anwenden:
   
Auf den folgenden Seiten werden die Gleichungen ausführlich gelöst.

Anmerkung: Die Probe ist nötig

Bei Anwendung des 1. und 2.Logarithmusgesetzes auf eine Logarithmusgleichung
können Lösungen hinzukommen. Daher ist es nötig ein Probe zu machen.
Allerdings haben wir uns ja bereits darauf geeinigt, beim Lösen von
Logarithmusgleichungen stets ein Probe zu machen.