Das 1. und 2.Logarithmusgesetz in Gegenrichtung

Das Problem: Lösungen gehen verloren

In diesem Kapitel geht es um die Anwendungen des 1. und 2.Logarithmusgesetzes:
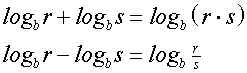
wpeF.jpg (4307 Byte)
Bis jetzt haben wir die Gesetze in der Leserichtung "von links nach rechts" benutzt, um
mehrere Logarithmen zusammenzufassen. Wir mussten jedoch immer eine Probe machen,
denn beim Anwenden der Gesetze in dieser Leserichtung können Lösungen hinzukommen.

Nun wollen wir uns fragen, ob wir die Formeln auch auch in der anderen Richtung
anwenden dürfen, also in der Leserichtung von "rechts nach links".
Wenn wir die beiden Gesetze "von rechts nach links"anwenden, dann müssen wir auf-
passen, denn dabei können Lösungen verlorengehen, wie das folgende Beispiel zeigt:
 

Beispiel: Eine Lösung verschwindet

Nun betrachten wir ein Beispiel bei dem Lösungen verlorengehen, weil wir das
1. Logarithmusgesetz in der umgekehrten (falschen) Richtung anwenden.
Gegeben ist die Logarithmusgleichung:

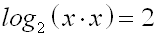
Nun machen wir den Fehler, und wenden wir das 1.Logarithmusgesetzl in der falschen Richtung an:
Dadurch wird der Logarithmus in die Summe zweier Logarithmen zerlegt:

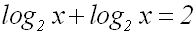
Auf der linken Seite kann man die beiden gleichen Summanden zusammenfassen:

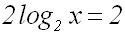
Wir teilen die Gleichung durch 2:

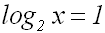
Nun wenden wir die Definition des Logarithmus an, so wie wir es im Kapitel 1 gelernt haben:

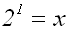
Die Potenz kann man ausrechnen. Wir erhalten die Lösung:

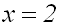
Die Lösung x=2 ist zwar richtig, aber die gegebene Gleichung hat zwei Lösungen: x=2 und x= –2.
Dies kann man überprüfen, indem man x=2 und x= –2 in die gegebene Gleichung einsetzt.
Es ist also während der Rechnung die Lösung x= –2 verloren gegangen.

Wir werden uns also überlegen müssen, wie wir diesen Fehler vermeiden können.