|
|
Wir kennen bereits das das 1. bzw. 2. Logarithmusgesetz:
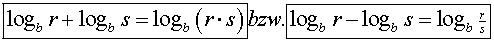
Wir wissen auch, dass in der Richtung "von rechts nach links" Lösungen verloren gehen
können.
Um dies zu verhindern, müssen wir wissen, warum
dabei
Lösungen verlorengehen: |
Durch die Anwendung der
beiden Gesetze in der falschen Richtung kann sich
der Defintionsbereich verkleinern, und dann gehen alle Lösungen verloren,
die in dem fehlenden Bereich lagen.
|
|
Als Beispiel betrachten wir die folgende Gleichung
mit dem Definitonsbereich R*, d.h.
der Defintionsbereich besteht aus allen reellen Zahlen ohne die Zahl
Null:
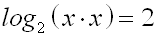
Nach Anwendung der 1.Logarithmusformel in der Richtung "von
rechts nach links" verkleinert sich
der Definitionsbereich auf R>0, d.h. auf die
positiven reellen Zahlen ohne Null:
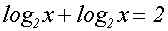
|
| Problemlösung durch Betragszeichen: |
Die Lösung des Problems besteht nun darin, dass man
Betragszeichen um die Variable x setzt,
sodaß der Definitionsbereich sich nicht mehr verkleinert, und somit keine Lösungen
verloren gehen: |
|
Wir betrachten wieder unser problematisches Beispiel von den vorigen beiden Seiten.
Man beachte, dass der Definitionsbereich aus allen rellen Zahlen außer Null
besteht: D=R\{0}
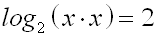
Wir benutzen das1.Lösungsgesetz in falschen Richtung:
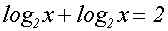 FALSCH FALSCH
Der Definitionsbereich verkleinert sich dadurch auf die positiven reellen Zahlen
ohne Null: D=R+\{0}
Wenn wir stattdessen Betragzeichen setzen, bleibt der Definitionsbereich D=R\{0} erhalten,
und deshalb können auch keine Lösungen verloren gehen:
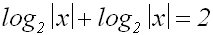 RICHTIG RICHTIG
Die beiden Summanden können wir zusammenfassen:
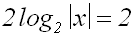
Wir teilen die Gleichung durch 2:
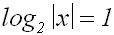
Nun wenden wir die Definition des Logarithmus an, so wie wir es im Kapitel
1 gelernt
haben:
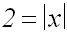
Wir lösen die Betragsgleichung, und erhalten:
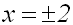
Wir sehen: Die Lösung x=–2, die im Beispiel
von der vorletzten Seite verloren ging, geht nun
nicht mehr verloren, weil wir dafür gesorgt haben, dass sich der Definitonsbereich nicht
verkleinert. |
|
|